Session 6: Distance - Module C: Traveling Salesman Problem

1. Discussion

What is the traveling salesman problem?
What makes it a difficult problem to compute?

2. Try It Out!

We've set up a traveling salesman problem with a few points outside. Your challenge is to come up with a good guess at the shortest route which visits each point once then returns to the starting point. You'll split up into teams of 2-3 people, then we'll head outside!

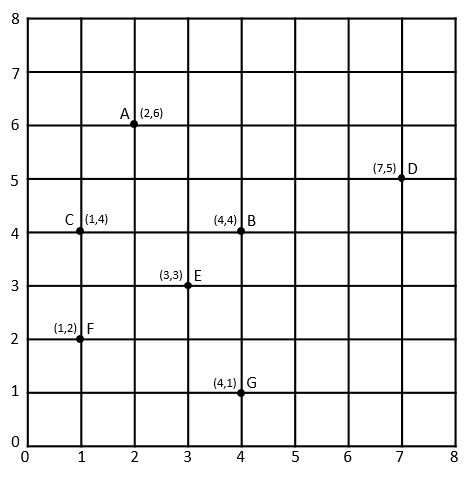
This is a map of the points we will be using!

3. Traveling Salesman Code


  1. Download the program tsp.py to your programs folder.
  2. Open the program in gedit so you can edit it.

Before you can use the program you'll need to make several changes to the code.

  1. Add the coordinates for each of the points from earlier to the beginning of the program. You should create a new variable for each point.
  2. Add each of the point variables to the points dictionary. Use a label (such as 'A') as the key and the corresponding variable as the value for each point.
  3. It's also a good idea to give the graph a title so it's easy to tell what the plot represents. Edit the line drawTSPPoints(points) to give the plot a title:

    drawTSPPoints(points, title="YOURTITLEHERE")

    A good title might be something like 'Traveling Salesman Problem'.
  4. Add your route to the program. List the points in order in the pathGuess list.

Go ahead and run the program from IPython! You should see the points displayed, along with your path. The program will also calculate and tell you the total distance for the route.

The rest of the code in the program calculates the shortest route. Go ahead and take a look at this code if you'd like! Does anything in this code look familiar to you? (Hint: Recall the 2D distances lesson.)

Uncomment the last line of the program to display the shortest route by erasing the hash symbol. Save your program then run it again. You should see your route as well as the calculated shortest path.

Be sure to save the plot to add to your website and answer these questions on your webpage! Also include the answer to this question: How close was your guess to the calculated solution?