Session 2: Sequences and Series - Module C: Fibonacci Sequence
1. Overview
What is the Fibonacci sequence?
What is its relevance?
Practice programming for loops
Code the Fibonacci Sequence
2. Fibonacci Sequence & Fibonacci Numbers
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, ...
3. The mechanics of Fibonacci:
Base Case:
Start with [0,1]
Step:
Add the previous two numbers
4. Golden Ratio:
The result of dividing the larger of the two Fibonacci numbers by the smaller number approaches the same number.
This special number is 1.618…
This number has been called Phi by the Greeks even before the Fibonacci numbers.
This golden ratio constantly shows up in nature and math.
The population experiments with rabbits, drawing perfect rectangles, drawing perfect spirals, maximizing seed growth and sunlight caught by pedals, and more!
Due to the benefits of having a flower’s pedals and seeds grow at angles with this ratio, Fibonacci numbers show up consistently in nature. Most flowers, fruits, and other plants show patterns with Fibonacci numbers.
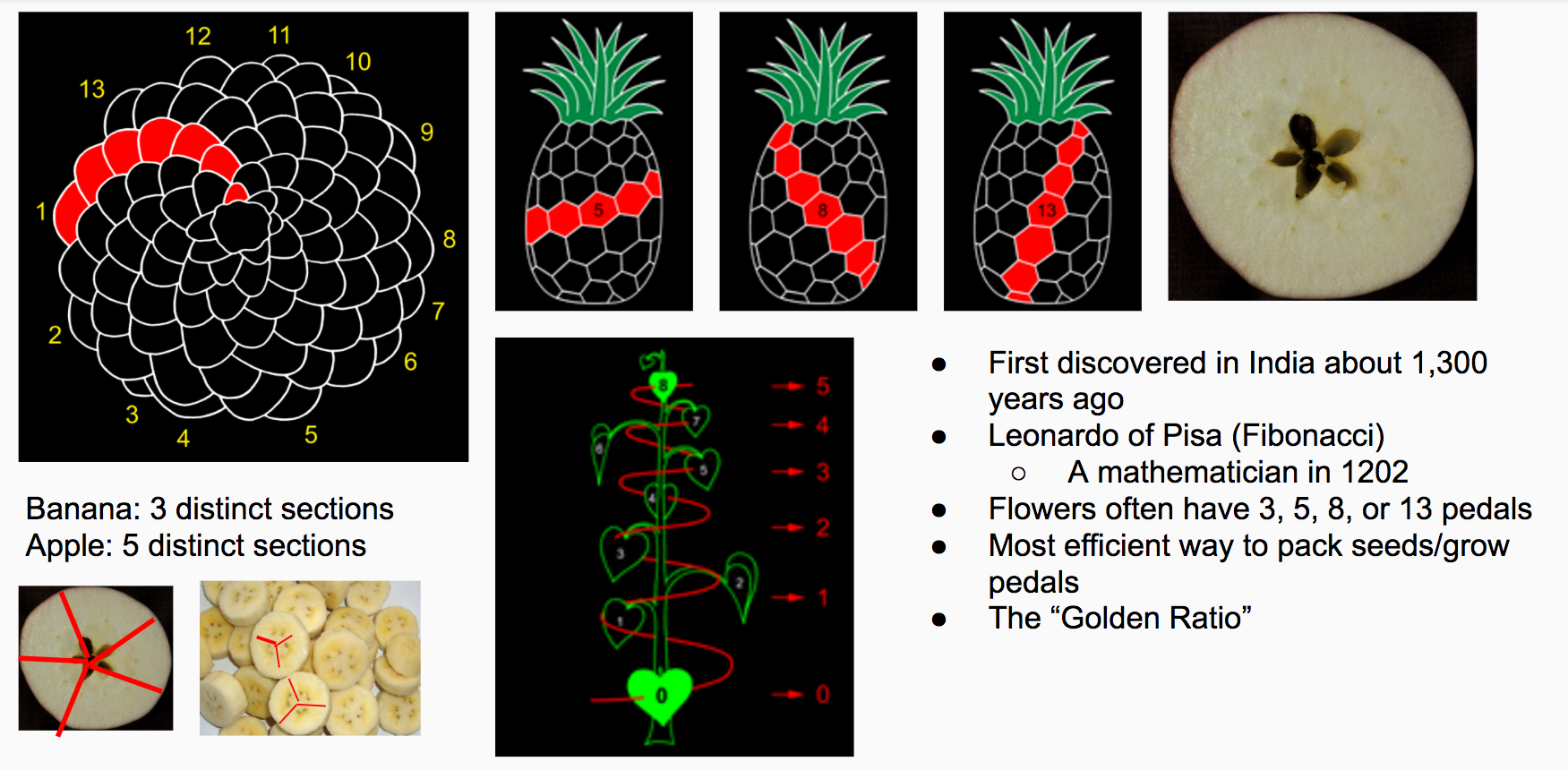
Count the spirals on a pineapple, the spirals on an acorn, and the spirals in a sunflower’s seeds. You will get a Fibonacci number!
It would be hard, or maybe more annoying to count even the 15th Fibonacci number.
We can use our programming tools to do this!
5. Lists & Loops:
First let’s get some more practice with lists and loops.
- Download the program fibLoops.py into your programs directory. Remember to add the .py to the end of the program so you can open it in ipython once you're done
- Open the terminal window.
- Change the directory to your programs directory with the cd command.
- Use ls to make sure that fibLoops.py is in the correct directory.
- Open fibLoops.py in gedit using: gedit fibLoops.py &
- Read the instructions and write the code after the "Code goes here: " comment!
-
If you finish the first two examples early feel free to work on the bonus problem at the bottom of fibLoops
Start by trying to code the first for loop.
There are examples on this page that you can experiment with! Don't be afraid to copy the code into your program and play around with it. In the second exercise we will try to code the Fibonacci Sequence. It might be a good idea to get out a scratch piece of paper and add up the first four or five numbers. Notice how each number changes both the variables! Remember to ask questions if you get stuck! We are always here to help.
To test your code follow these instructions:
- Start IPython with the ipython command.
- From Ipython, you can run your program by typing run fibLoops.py.
- Test out each exercise in your terminal before moving on to the next exercise. That way, if it doesn't work, it's a lot easier to figure out what's going on!
When you are done with the final exercise (or the bonus exercise) take a picture of your output and please answer these questions on your webpage.
